太陽電池の出力特性と最大電力点(MPP)
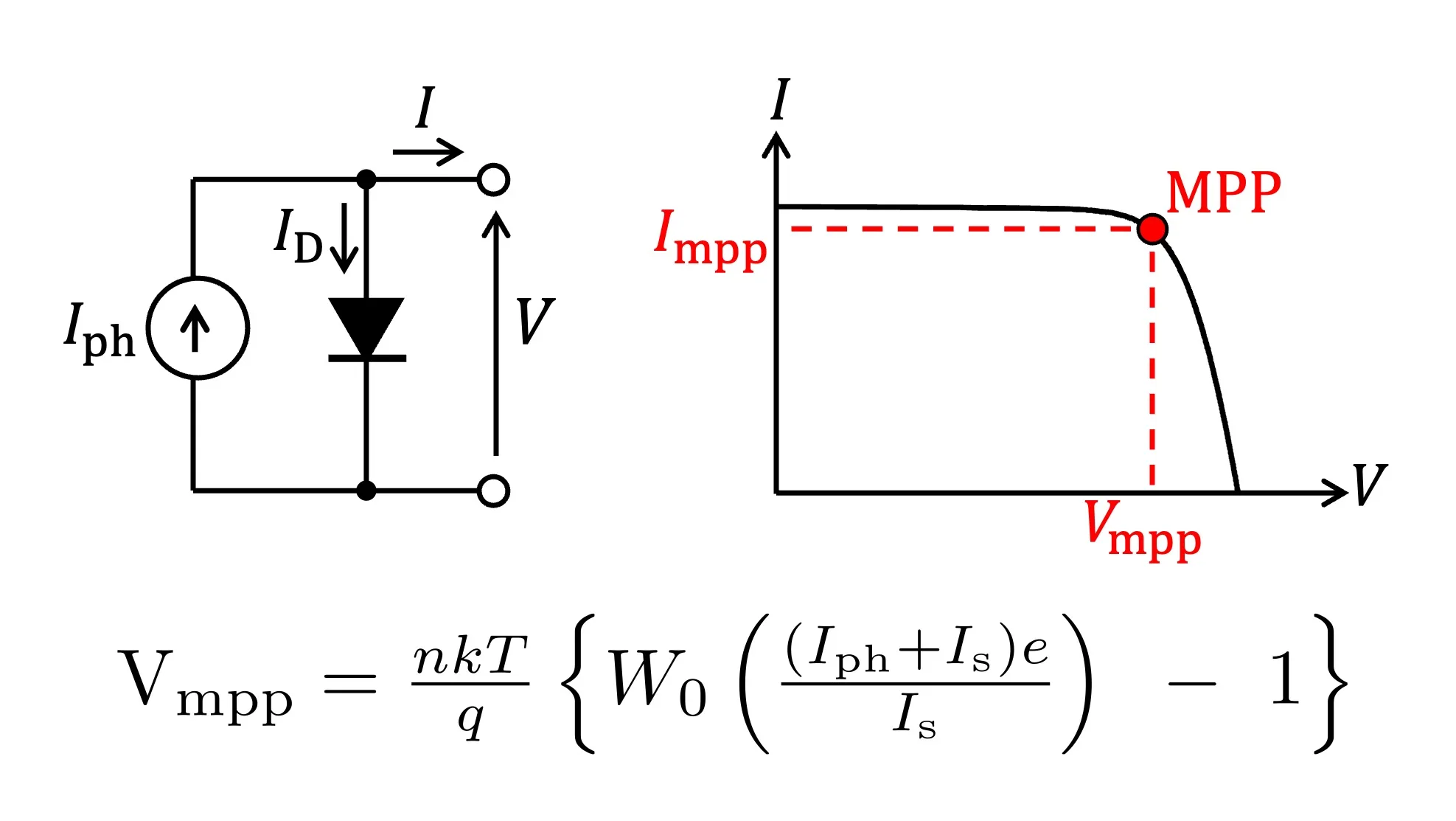
太陽電池はFig.1 (a)に示す電流-電圧特性($I$-$V$特性)を有しています。また、この$I$-$V$特性より電力-電圧特性($P$-$V$特性)を求めるとFig.1 (b)となります。
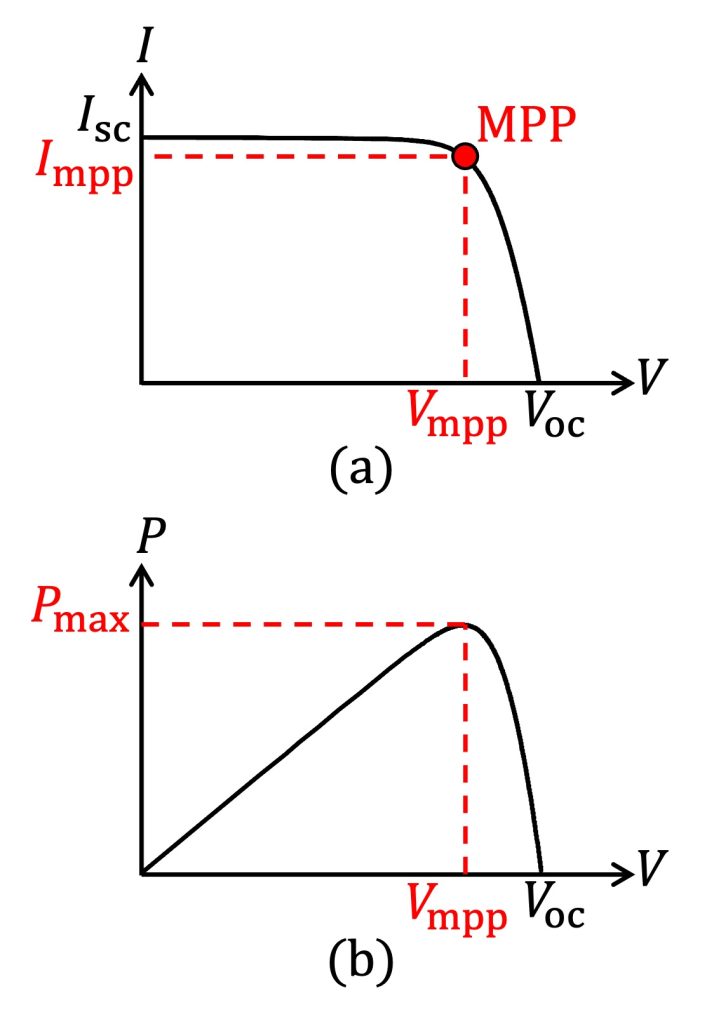
(a) $I$-$V$特性 (b) $P$-$V$特性
Fig.1 太陽電池の有する出力特性の概形
Fig.1 (b)より、太陽電池は出力電力が最大となる動作点$(I_{\rm mpp},V_{\rm mpp})$を持ちます。この動作点は最大電力点(MPP: Maximum Power Point)と呼ばれ、太陽電池を最大効率で利用するためにはMPPにて電力を取り出す必要があります。また、太陽電池の$I$-$V$特性は日射強度や温度に対して依存性を持ち、日射強度・温度が変動すると最大電力点も変化します。
等価回路パラメータによる最大電力点の表現
太陽電池の出力特性は等価回路モデルにて表現されます。本章では、等価回路パラメータにて最大電力点がどの様に表されるのかについて説明します。太陽電池の等価回路モデルについては以下の記事で詳細に解説を行っていますので、是非併せてご参照下さい。
理想的には、太陽電池の出力特性はFig.2に示す電流源とダイオードからなる等価回路にて表されます。
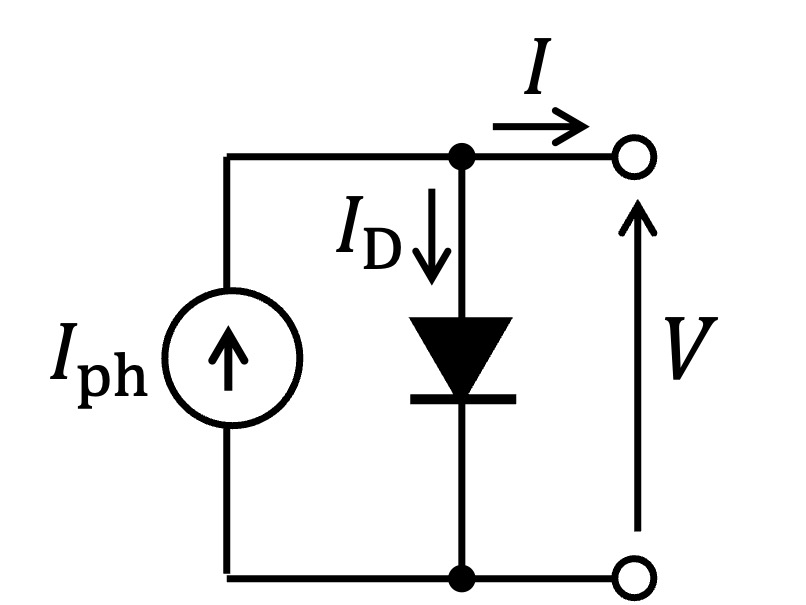
Fig.2 太陽電池の理想等価回路モデル
この等価回路モデルにおいて、$I$-$V$特性はEq.(1)にて表されます。Eq.(1)において、$I_{\rm s}$は逆方向飽和電流、$n$はダイオードの理想係数、$k$はボルツマン定数、$q$は電気素量、$T$は絶対温度です。
$$I = I_{\rm ph} ~ – ~ I_{\rm s} \left \{ {\rm exp}\left( \frac{q V }{nkT} \right) -1 \right \} \tag{1}$$
また、電圧$V$における太陽電池の出力電力$P(V)$は
$$P(V) = IV = \left [ I_{\rm ph} ~ – ~ I_{\rm s} \left \{ {\rm exp}\left( \frac{q V }{nkT} \right) -1 \right \} \right ] V \tag{2}$$
であり、MMPにおいて$P(V)$は最大値をとります。そこで、Eq.(1)とEq.(2)を用いて$P$が極大となる$V$を調べます。$P$を$V$で微分すると
$$ \frac{d P(V)}{d V} = I_{\rm ph} + I_{\rm s} ~ – ~ I_{\rm s} \left ( 1+ \frac{ q V }{nkT} \right ) {\rm exp}\left( \frac{q V }{nkT} \right) \tag{3}$$
となります。ここで、$P$が極値となる$V$($=V_{\rm mpp}$)は
$$ \left . \frac{d P(V)}{d V} \right |_{V=V_{\rm mpp}} = 0 \tag{4}$$
をみたすときであり、Eq.(3)とEq.(4)より最大電力点電圧$V_{\rm mpp}$が満たす条件として次式に示す超越方程式を得ます。
$$ \frac{ I_{\rm ph} + I_{\rm s} }{ I_{\rm s} } = \left ( 1+ \frac{ q V_{\rm mpp} }{nkT} \right ) {\rm exp}\left( \frac{q V_{\rm mpp} }{nkT} \right) \tag{5}$$
Eq.(5)は$V_{\rm mpp}$について初等的に解くことはできませんが、ランベルトのW関数と呼ばれる特殊関数を用いると、$V_{\rm mpp}$は次式のように解析的に表すことができます。ここで、$W_0$はランベルトのW関数の主枝です。
$$ V_{\rm mpp} = \frac{nkT}{q} \left \{ W_0 \left( \frac{ ( I_{\rm ph} + I_{\rm s}) e }{ I_{\rm s} } \right) ~ – ~ 1 \right \} \tag{6}$$
ランベルトのW関数については以下の記事で詳細に解説していますので、併せてご覧下さい。
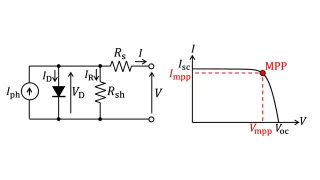
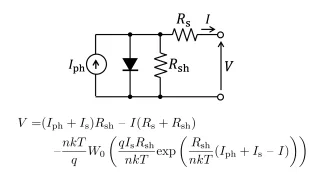
なお、実際の太陽電池には並列寄生抵抗$R_{\rm sh}$および直列寄生抵抗$R_{\rm s}$が存在します。これらを考慮した等価回路モデルをFig.3に示します。
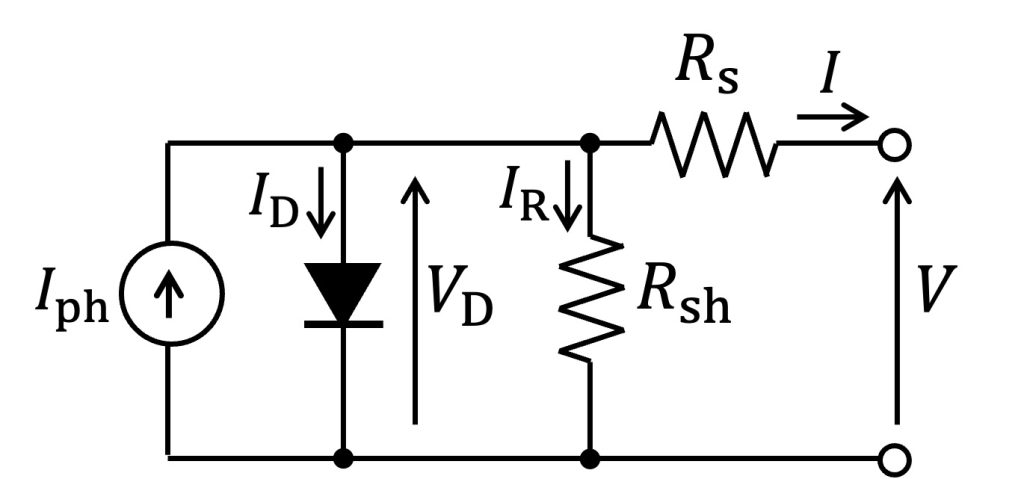
Fig.3 寄生抵抗を考慮した太陽電池の等価回路モデル
寄生抵抗を無視したFig.2の等価回路モデルの場合、最大電力点はEq.(6)に示したようにランベルトのW関数を用いることで解析的に表現することが可能でした。しかし、Fig.3の寄生抵抗を考慮した回路モデルの場合、最大電力点を解析的に求めることはできません。Fig.3の回路モデルより、最大電力点におけるダイオード電圧$V_{\rm D(mpp)}$に関する超越方程式としてEq.(7)が求まります[1]。ここで、Eq.(7)における$I \left ( V_{\rm D (mpp)} \right )$はEq.(8)にて与えられます。
$$ \begin{align}
&\begin{split} 0 = & \left \{ 2 R_{\rm s} R_{\rm sh} I_{\rm s} {\rm exp}\left( \frac{q V_{\rm D (mpp)} }{nkT} \right) + \left ( 2 R_{\rm s} + R_{\rm sh} \right ) \frac{q V_{\rm D (mpp)} }{nkT} \right \} I \left ( V_{\rm D (mpp)} \right ) \\
& \quad \quad ~ – ~ V_{\rm D (mpp)} \left ( R_{\rm sh} I_{\rm s} {\rm exp}\left( \frac{q V_{\rm D (mpp)} }{nkT} \right) + \frac{q V_{\rm D (mpp)} }{nkT} \right ) \end{split} \tag{7} \\[1.5em]
& \quad I \left ( V_{\rm D (mpp)} \right ) = I_{\rm ph} ~ – ~ I_{\rm s} \left ( {\rm exp} \left( \frac{q V_{\rm D (mpp)} }{nkT} \right) ~ – ~ 1 \right ) ~ – ~ \frac{V_{\rm D (mpp)}}{R_{\rm sh} } \tag{8} \end{align}$$
前述の通り、上式を解析的に解くことはできませんが、Eq.(7)を$V_{\rm D (mpp)}$について数値的に解き、次式に代入することで最大電力電圧$V_{\rm mpp}$を求めることが可能です。
$$ V_{\rm mpp} = V_{\rm D (mpp)} ~ – ~ R_{\rm s} I \left ( V_{\rm D (mpp)} \right ) \tag{9}$$
最大電力点と日射強度・温度の関係
太陽電池の$I$-$V$特性は日射強度・温度の関数であるため、最大電力点は日射強度・温度が変化すると変動します。$I$-$V$特性の日射強度・温度特性は、$I$-$V$特性のモデル式に含まれる温度$T$に加えて、等価回路パラメータ$I_{\rm s}$の温度依存性および$I_{\rm ph}$の日射強度依存性により表現されます。これらについては以下の記事にて詳細に解説しておりますので、興味のある方は併せてご覧下さい。
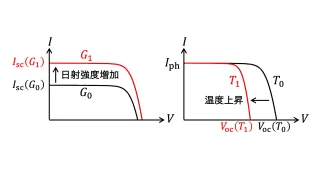
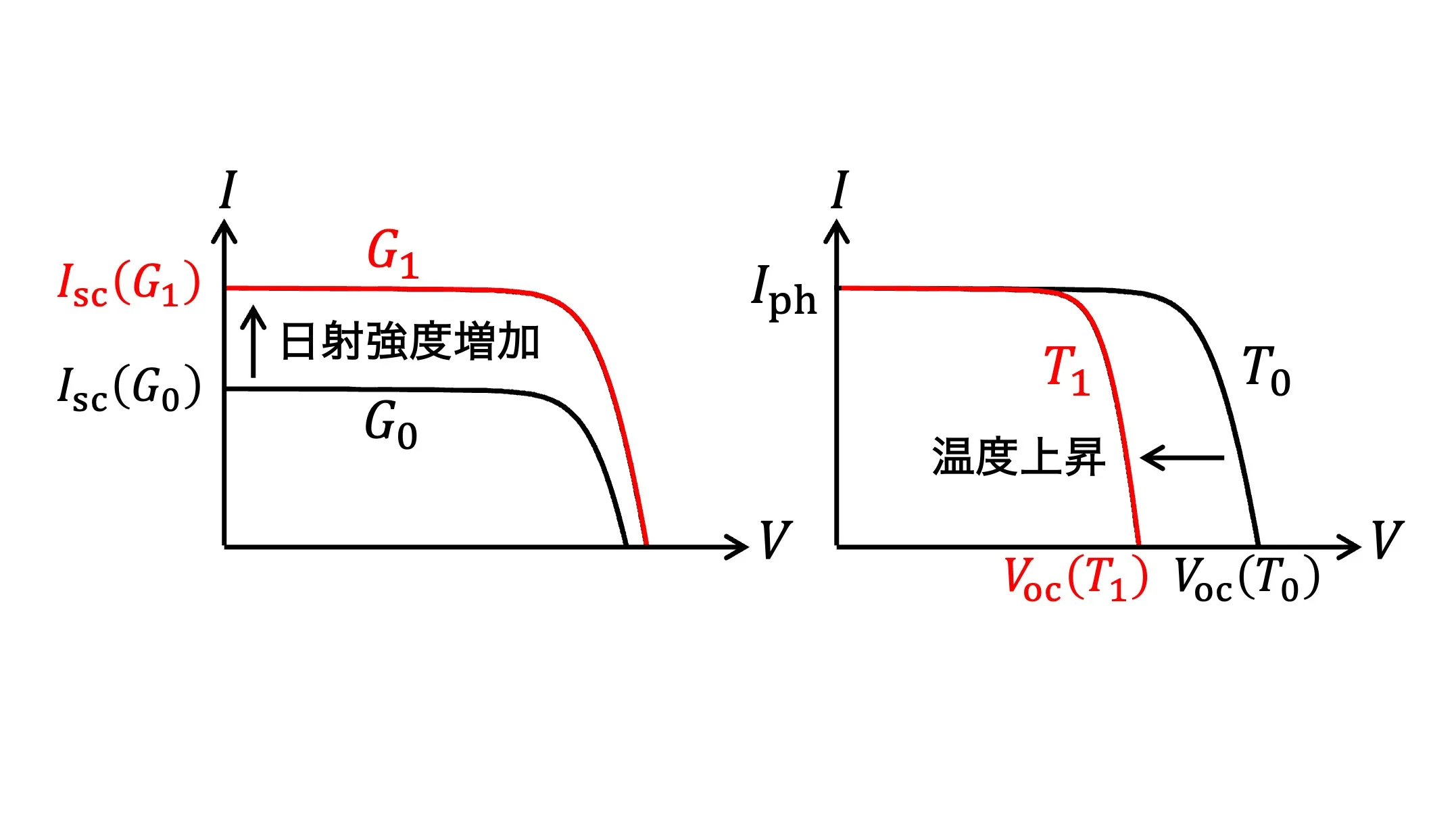
日射強度および温度に対する$I$-$V$特性の依存性を図示すると、Fig.4 (a-1),(b-1)のようになります。また、$I$-$V$特性より$P$-$V$特性を求めると、Fig.4 (a-2),(b-2)となります。Fig.Fig.4において$G$は日射強度$(G_0 < G_1)$、$T$は温度$(T_0 < T_1)$を表します。
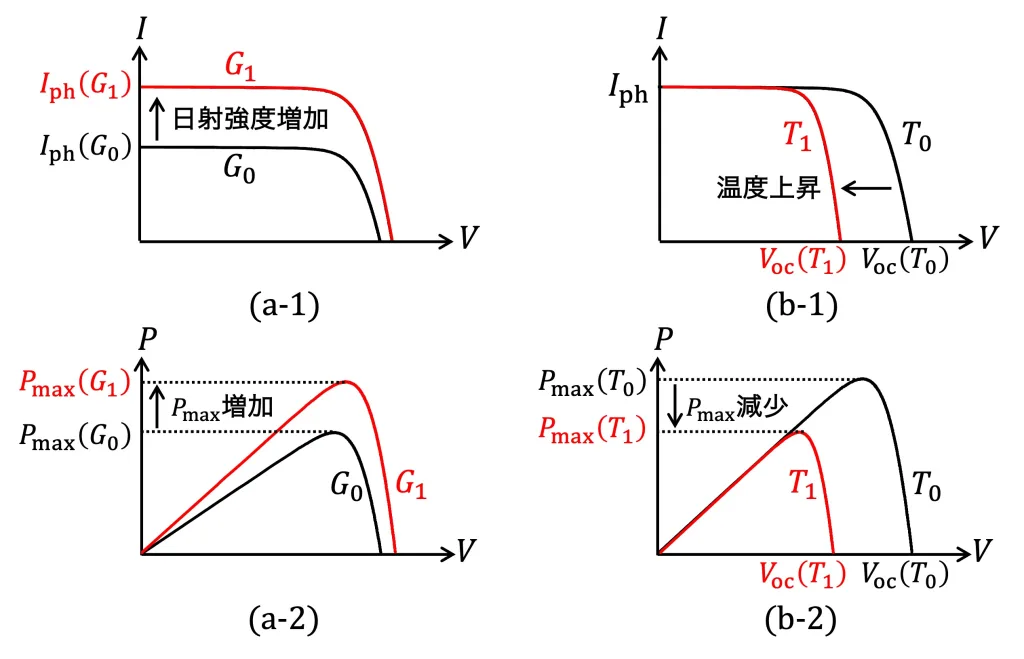
(a-1,2) 日射強度$G$上昇時の変化 (a-1,2) 温度$T$上昇時の変化
Fig.4 太陽電池の$I$-$V$特性・$P$-$V$特性と日射強度$G$・温度$T$の関係
Fig.4 (a)に示すように日射強度が増加すると最大電力点電流が上昇し、最大取得電力$P_{\rm max}$が増加します。一方で、Fig.4 (b)のように温度が増加すると最大電力点電圧が低下し、最大取得電力$P_{\rm max}$が減少します。そのため、太陽電池の能力を最大限に利用するためには最大電力点追従(MPPT: Maximum Power Point Tracking)と呼ばれる、動作点を最大電力点に保つ制御を行う必要があります。最大電力点追従を行うことで、日射強度・温度によらず常に最大の電力を太陽電池から取得することができ、太陽電池を効率的に利用することが可能となります。
MPPTを行う方法(アルゴリズム)は複数存在し、代表的なものとして$P$-$V$特性上を手探り的に探索する山登り法がよく用いられます。また、前節で示したように太陽電池の等価回路パラメータが既知であれば、最大電力点を等価回路パラメータより計算(推定)することが可能です。これを用いたMPPT制御として、等価回路モデルベースでスキャンレスかつ高速な最大電力点追従を行う「I-V特性推定型MPPT」が提案されています[1]。
なお、最大電力点に対する動作点の一致度合いは出力利用率(UUF: Useful utilization Factor)という指標で評価されます。ある動作点の出力電力を$P_{\rm op}$とすると、その動作点のUUFは次式により計算されます[2]。
$$ {\rm UUF} = \frac{ P_{\rm op} }{ P_{\rm mpp} } = \frac{ V_{\rm op} I_{\rm op} }{ V_{\rm mpp} I_{\rm mpp} } \tag{9}$$
MPPT制御については、後日別途解説を行います。
まとめ
太陽電池には最大電力点と呼ばれる、取得電力が最大となる動作点が存在します。本記事では、太陽電池の等価回路モデルに基づいて最大電力点が等価回路パラメータにより表現できることを示しました。
最大電力点は日射強度・温度に応じて変化するため、太陽電池の効率的利用には動作点を最大電力点に保つ最大電力点追従制御(MPPT制御)を行う必要があります。MPPT手法は複数存在し、山登り法と呼ばれる古典的な極値探索手法が良く用いられます。
参考文献
[1] 池野孝, 内海淳志, 平地克也, 中川重康, “太陽電池の等価モデルを用いたI-V特性推定型MPPTの提案,” 電気学会論文誌B, vol.138, no.8, pp.514-520, 2018.
DOI:10.1541/ieejpes.138.514
[2] 板子一隆, 森武昭, “独立型太陽光発電システムにおける最大電力点追跡のための一制御方式,” 電気学会論文誌D, vol.123, no.12, pp.1537-1543, 2003.
DOI:10.1541/ieejias.123.1537



コメント