日射強度・温度が太陽電池のI-V特性に与える影響

等価回路モデルとパラメータの日射強度・温度依存性
I-V特性の日射強度依存性
I-V特性の温度依存性
まとめ
参考文献

等価回路モデルとパラメータの日射強度・温度依存性

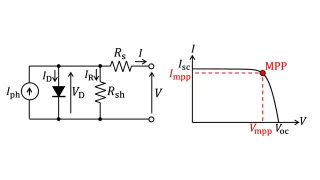
　太陽電池の出力特性はFig.1に示す等価回路としてモデル化されます。Fig.1において$I_{\rm ph}$は光電流、$V_{\rm D}$は内部ダイオードの両端電圧を表します。また、$R_{\rm s}$は直列寄生抵抗、$R_{\rm sh}$は並列寄生抵抗です[1]。

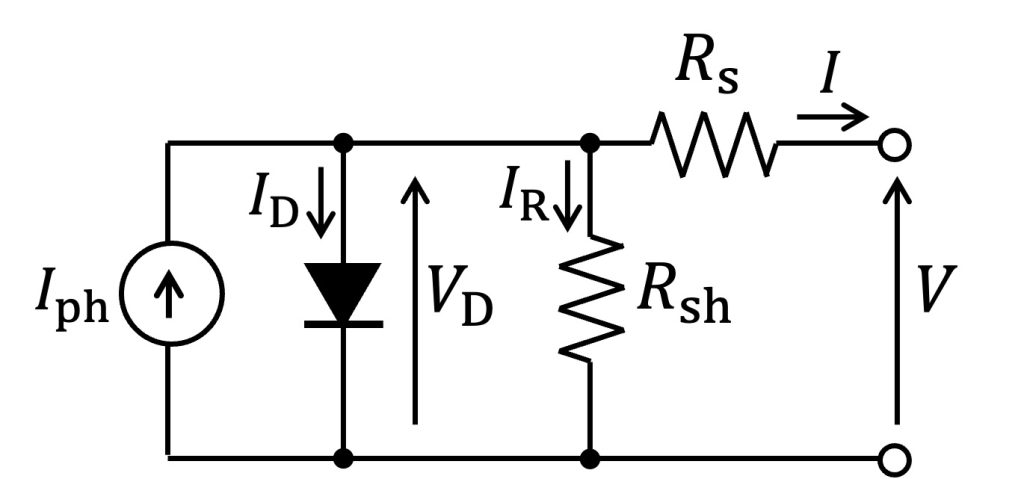
Fig.1 太陽電池の等価回路モデル

太陽電池の等価回路モデルについては以下の記事で詳細に解説を行っていますので、是非併せてご参照下さい。

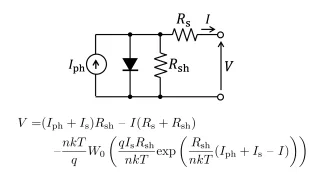
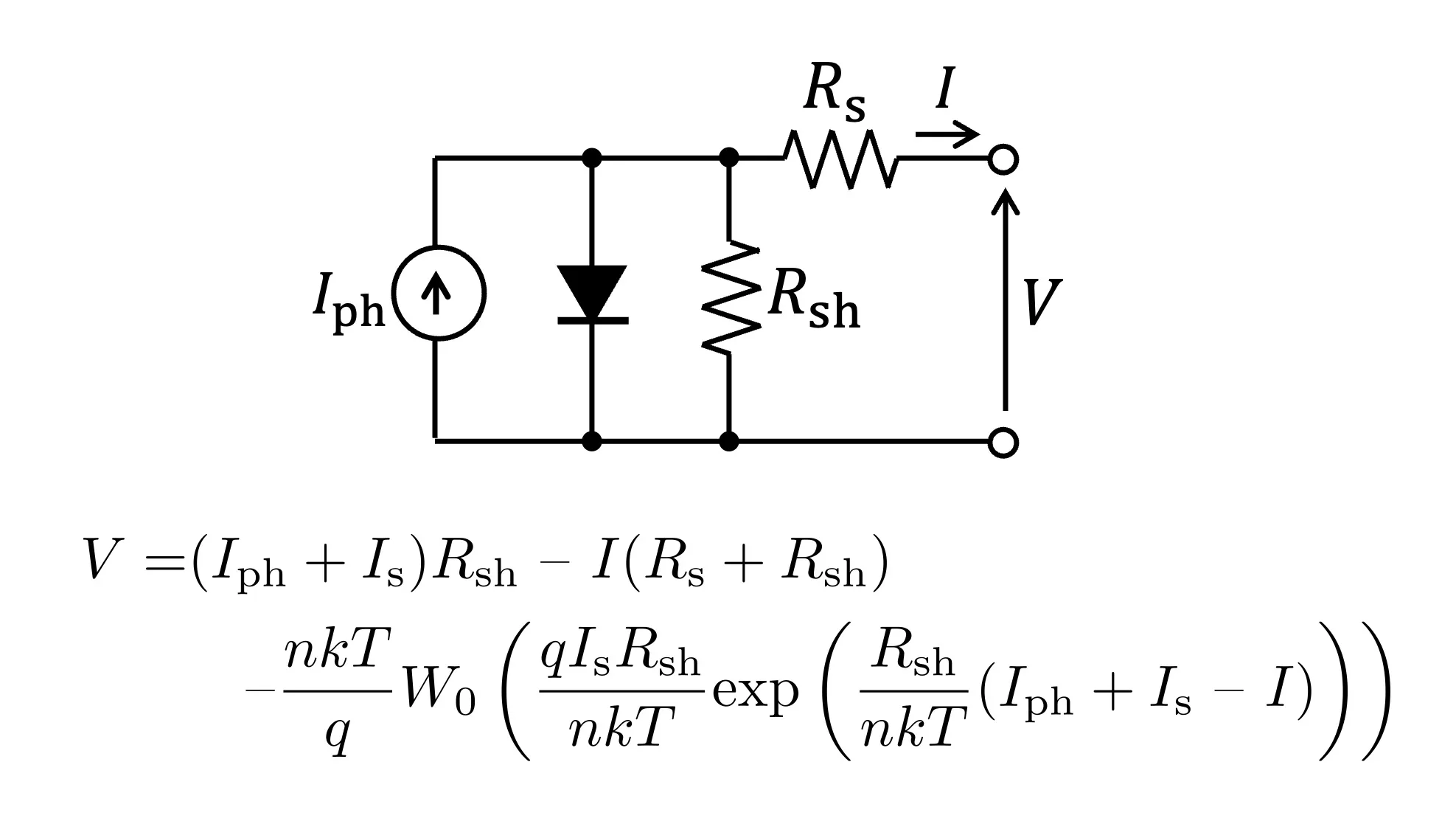
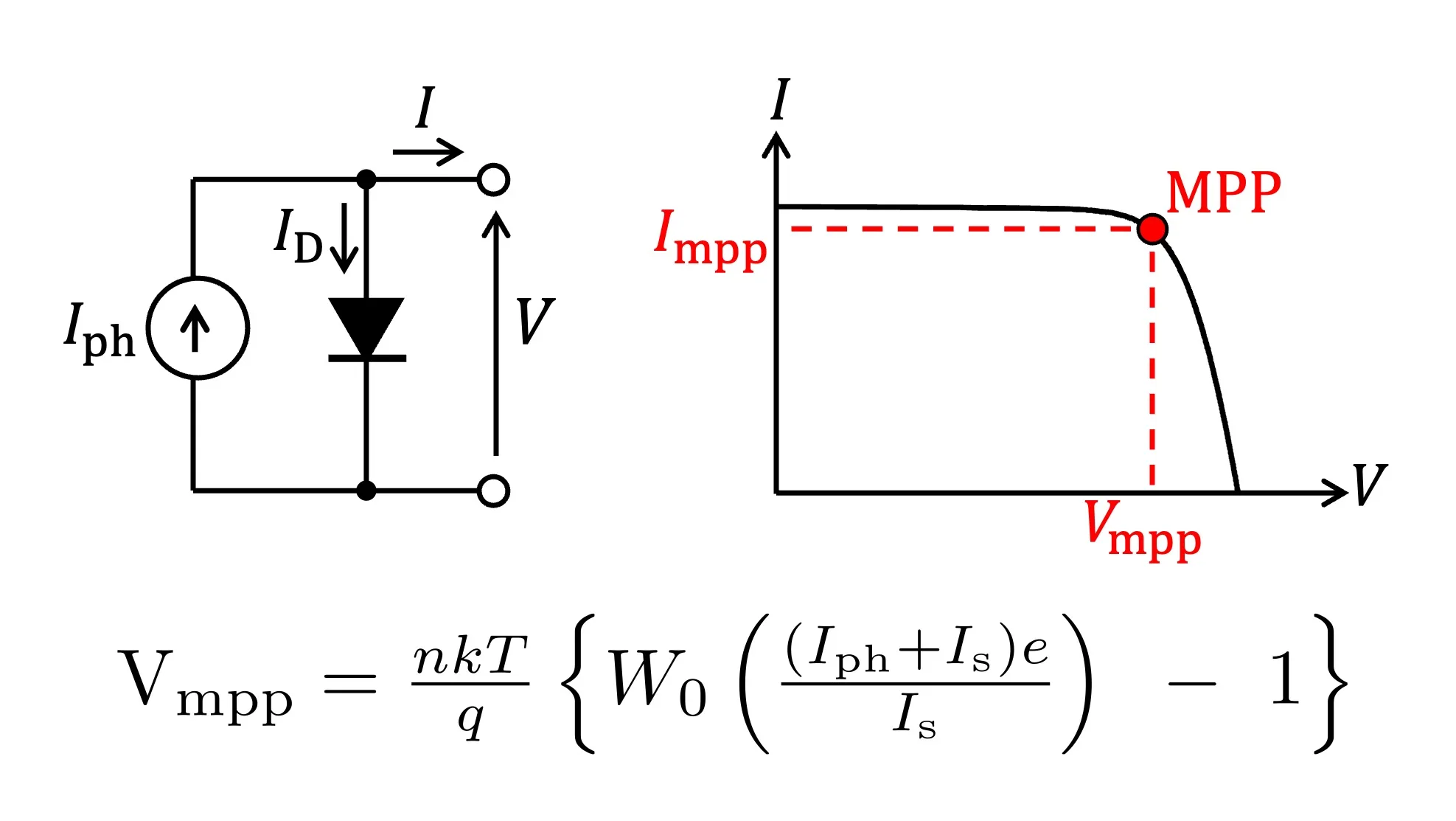
本記事では、見通しを良くするためにFig.1の等価回路モデルにおいて$R_{\rm s}=0$、$R_{\rm sh}=\infty$と近似した簡易等価回路モデルを用いて、日射強度・温度と$I$-$V$特性の関係を説明します。簡易等価回路モデルをFig.2に示します。

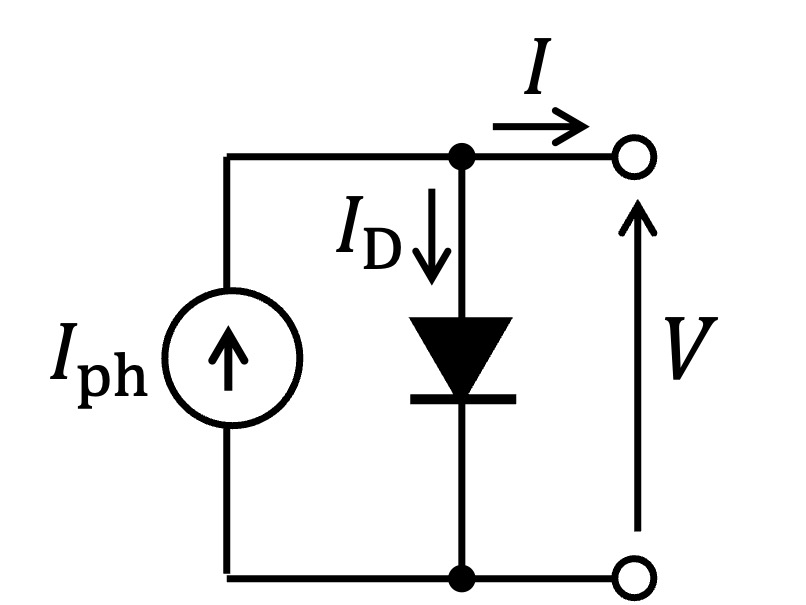
Fig.2 太陽電池の簡易等価回路モデル($R_{\rm s}$と$R_{\rm sh}$を無視)

簡易等価回路モデルの$I$-$V$特性はEq.(1)にて表されます。Eq.(1)において、$I_{\rm s}$は逆方向飽和電流、$n$はダイオードの理想係数、$k$はボルツマン定数、$q$は電気素量、$T$は絶対温度です。

$$I = I_{\rm ph} ~ – ~ I_{\rm s} \left \{ {\rm exp}\left( \frac{q V }{nkT} \right) -1 \right \} \tag{1}$$

Eq.(1)において$I_{\rm ph}$は日射強度$G$、$I_{\rm s}$は絶対温度$T$の関数であり、それぞれはEq.(2), (3)としてモデル化されます。各式において、$a$は日射強度に対する光電流の比例係数、$E_g$はバンドギャップネルギー(Siの場合は約1.12 eV)、$A$は物性によって決まる定数です。

$$ I_{\rm ph} (G)= a G \tag{2}$$

$$ I_{\rm s} (T)= A T^{ 3 } {\rm exp} \left( – \frac{E_g }{kT} \right) \tag{3}$$

これらをEq.(1)に代入することで、次式に示す温度$T$・日射強度$G$における$I$-$V$特性のモデル式を得ます。

$$I = a G ~ – ~ A T^{ 3 } {\rm exp} \left( – \frac{ E_g }{kT} \right) \left \{ {\rm exp}\left( \frac{q V }{nkT} \right) -1 \right \} \tag{4}$$

　なお、ランベルトのW関数と呼ばれる特殊関数を用いることで寄生抵抗$R_{\rm s}$、$R_{\rm sh}$を無視せずとも解析を行うことができますが、今回は理解をしやすくするためにあえて寄生抵抗を無視します。ランベルトのW関数については以下の記事で解説していますので、興味のある方は是非ご一読下さい。

I-V特性の日射強度依存性

　本章では、恒温状態下で日射強度$G$が変化した際に、$I$-$V$特性全体がどのように変化するのか解析します。等価回路モデルにて光電流は日射強度に依存性を持つため、日射変動の影響は$I$-$V$特性の電流$I$軸方向への変化として現れます。そのため、$I$-$V$特性の電流$I$に着目して説明を行います。
　Eq.(4)を日射強度$G$で偏微分すると

$$ \frac{\partial I}{\partial G} = a \tag{5}$$

となり、$I$の$G$に関する偏導関数は日射強度や温度に依存しない定数であることがわかります。これより、日射強度$G$が変化すると$I$-$V$特性は概形を保ったまま$I$軸方向に平行移動し、その変化量は日射強度の変動量に正比例します。
　なお、Eq.(3)より短絡電流$I_{\rm sc}$は光電流$I_{\rm ph}(G)$に一致するため、$I_{\rm sc}$と日射強度$G$の関係は次式にて表されます。

$$ I_{\rm sc} (G) = I_{\rm ph}(G) = a G \tag{6}$$

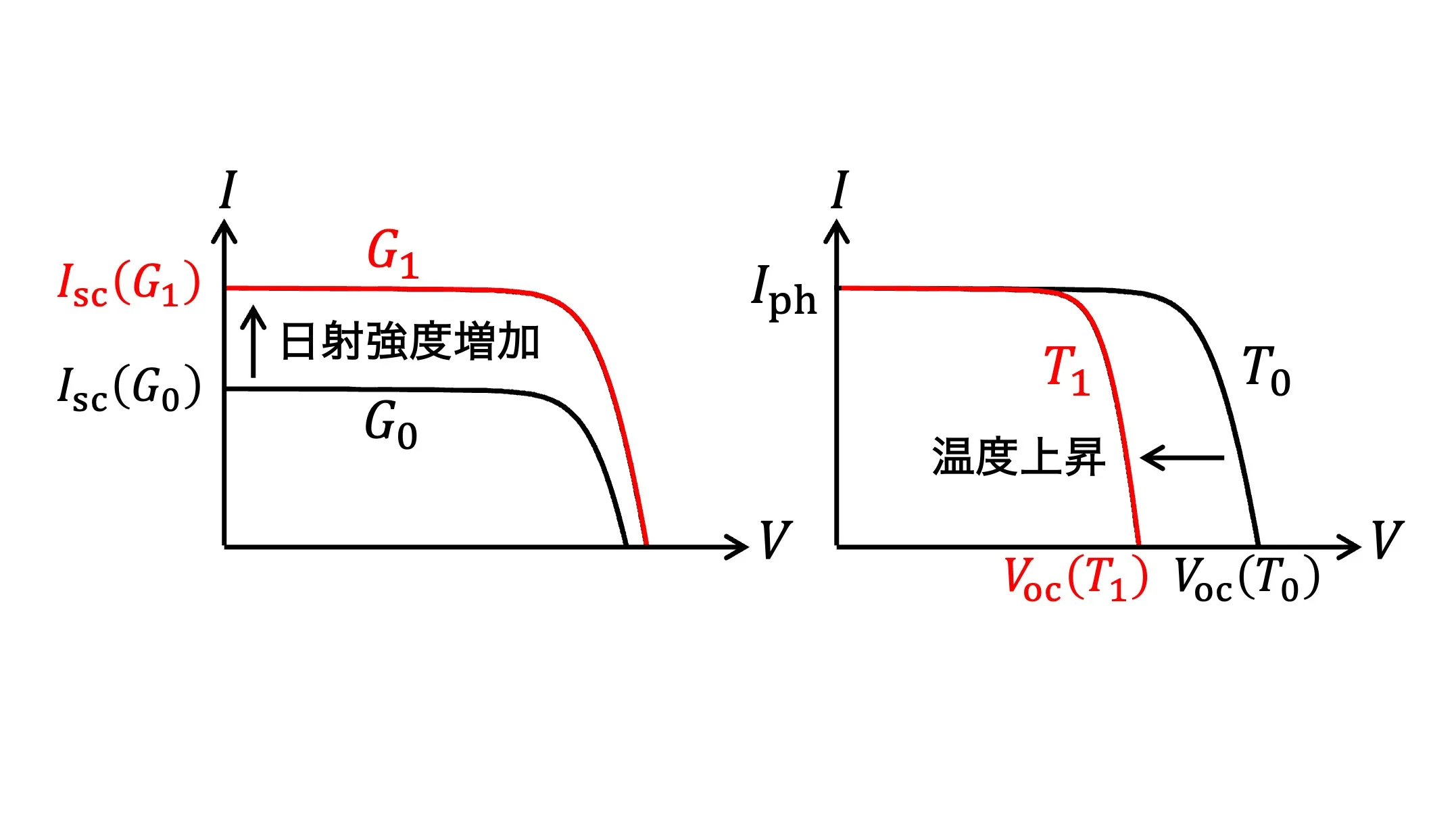
　これらの解析を基に、日射強度が増加した際における$I$-$V$特性の変化を図示するとFig.3 (a)となります。このとき、$P$-$V$特性はFig.3 (b)のように変化します。Fig.3において$G_0$、$G_1$は異なる日射強度であり、$G_0 < G_1$の関係を持つものとします。

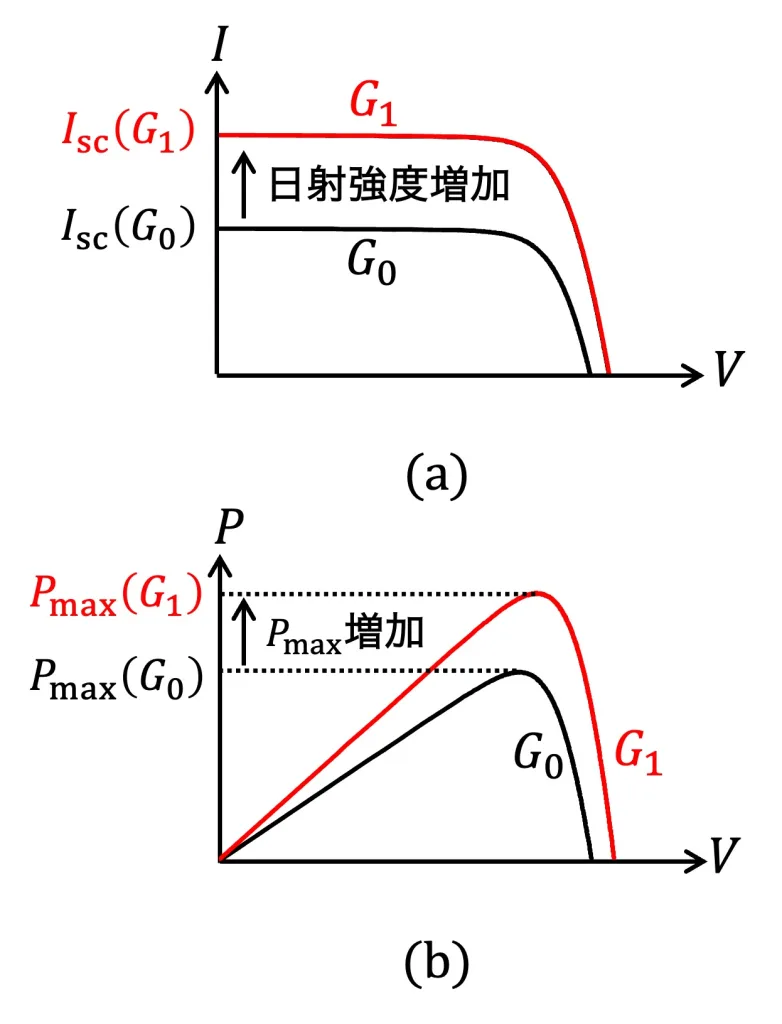
(a) $I$-$V$特性　(b) $P$-$V$特性
Fig.3　日射強度増加時$(G_0 \rightarrow G_1)$における出力特性の変化(温度$T$は一定とする)

Eq.(5),(6)より、Fig.3 (a)における$I_{\rm sc}$の変動量$I_{\rm sc} (G_1) ~ – ~ I_{\rm sc} (G_0)$は次式にて表されます。

$$ I_{\rm sc} (G_1) ~ – ~ I_{\rm sc} (G_0) = a (G_1 ~ – ~ G_0) \tag{7}$$

またFig.3 (b)より、日射強度が増加すると最大出力電力$P_{\rm max}$も増加します。このとき、最大電力点電圧$V_{\rm mpp}$は大きく変化しないため、$P_{\rm max}$は日射強度$G$におおよそ比例して増加します。すなわち、変動量$P_{\rm max}(T_1) ~ – ~ P_{\rm max} (T_0)$についておおよそ次式が成り立ちます。

$$ P_{\rm max}(G_1) ~ – ~ P_{\rm max} (G_0) \propto a (G_1 ~ – ~ G_0) \tag{8}$$

これらと同様に、日射強度が減少すると$I_{\rm sc}$は$G$に比例して減少し、それに伴って$P_{max}$もおおよそ比例する形で減少します。

I-V特性の温度依存性

　次に、日射強度が一定の条件下で温度$T$が変化した際における$I$-$V$特性を解析します。開放電圧に関する解析にて述べたように、開放電圧は主に温度$T$の影響を受けるため、温度変動の影響は$I$-$V$特性において電圧$V$軸方向の変化として現れます。したがって、日射強度とは逆に$I$-$V$特性の電圧$V$に着目すると理解しやすくなります。
　Eq.(3)において、解析的な取扱いを容易にするために$ {\rm exp}\left( q V /nkT \right) \gg 1$と近似することでEq.(9)を得ます。この近似は$I$-$V$特性上の短絡状態近辺($I \fallingdotseq I_{\rm ph}$)を除く広い領域において成立します。

$$I \fallingdotseq a G ~ – ~ A T^{ 3 } {\rm exp} \left( – \frac{ E_g }{kT} \right) {\rm exp}\left( \frac{q V }{nkT} \right) \tag{9}$$

Eq.(9)を出力電圧$V$について解き、対数関数を展開すると次式となります。

$$ \begin{split} V & = \frac{nkT}{q } {\rm ln} \left( \frac{ aG ~ – ~ I }{ A T^{ 3 } {\rm exp} \left( – \frac{ E_g }{kT} \right) } \right) \\[0.2em]
&= \frac{nkT}{q } {\rm ln} \left( \frac{ aG ~ – ~ I }{ A T^{ 3 } } \right) + \frac{n E_g }{q} \end{split} \tag{10}$$

ここで、Eq.(10)を温度$T$で偏微分すると

$$ \begin{split} \frac{\partial V}{\partial T} &= {\rm ln} \left( \frac{ aG ~ – ~ I }{ A T^{ 3 } } \right) ~ \frac{\partial }{\partial T} \left( \frac{nkT}{q} \right) + \frac{nkT}{q} \frac{\partial }{\partial T} {\rm ln} \left( \frac{ aG ~ – ~ I }{ A T^{ 3 } } \right) \\
&=\frac{nk}{q} {\rm ln} \left( \frac{ aG ~ – ~ I }{ A T^{ 3 } } \right) ~ – ~ \frac{ 3 nk }{ q } \end{split} \tag{11}$$

となります。Eq.(11)には出力電流$I$が含まれているので、ここにEq.(7)を代入することで次式を得ます。

$$ \begin{split} \frac{\partial V}{\partial T} &= \frac{nk}{q} {\rm ln} \left( {\rm exp} \left( – \frac{ E_g }{kT} \right) {\rm exp}\left( \frac{q V }{nkT} \right) \right) ~ – ~ \frac{ 3 nk }{ q } \\[0.2em]
&= \frac{1}{T} \left( V ~ – ~ \frac{n E_g}{q} \right) ~ – ~ \frac{ 3 nk }{ q } \end{split} \tag{12}$$

Eq.(12)のように、$V$の$G$に関する偏導関数は$V$を含むため、動作点毎に温度依存性(温度による影響の受けやすさ)が異なります。そのため、温度$T$が変化すると$I$-$V$特性の形状(曲線のかたち)が変化します。その中でも特徴的な動作点として解放電圧$V_{\rm oc}$に着目すると、常温($T = {\rm 300 K}$の近傍)のSi太陽電池では、$V_{\rm oc}$付近の温度依存性はおおよそEq.(13)に従います。
※$E_g = 1.12 ~{\rm eV}$(Siのバンドギャップエネルギー)とし、$V_{\rm oc} $は全セルの拡散電位の総和(1セルあたり0.5〜0.6 V程度)におおよそ一致するという仮定をしています。

$$ \left . \frac{\partial V}{\partial T} \right |_{V = V_{\rm oc}, ~ T= 300} \fallingdotseq -2n \ {\rm mV/K} \tag{13}$$

このように、一般に太陽電池の$I$-$V$特性は温度に対して負の依存性を持ちます。この負の温度依存性は、温度$T$が上昇すると$I$-$V$特性が電圧$V$軸の負方向におおよそシフトする現象として観測されます。
　なお、Eq.(4)より日射強度$G$、温度$T$における開放電圧$V_{\rm oc}$の厳密な値は次式にて表されます。

$$ V_{\rm oc} (T,G) = \frac{nkT}{q } {\rm ln} \left( \frac{ a G }{ A T^{ 3 } {\rm exp} \left( – \frac{ E_g }{kT} \right) } + 1 \right) \tag{14}$$

　解析結果を基に、温度上昇時における$I$-$V$特性の変化を図示するとFig.4 (a)となり、$P$-$V$特性はFig.4 (b)のように変化します。Fig.4において$T_0$、$T_1$は異なる温度であり、$T_0 < T_1$の関係を持つものとします。

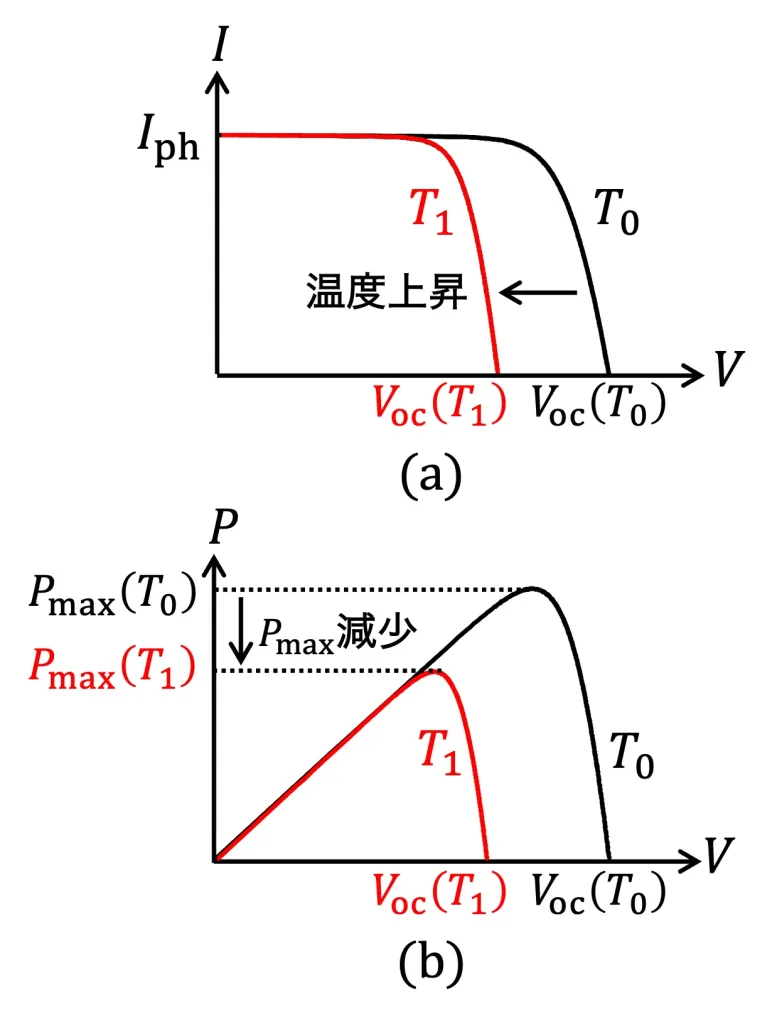
(a) $I$-$V$特性　(b) $P$-$V$特性
Fig.4　温度上昇時$(T_0 \rightarrow T_1)$における$I$-$V$特性の変化(日射強度$G$は一定とする)

Eq.(13)より、Fig.4 (a)における$V_{\rm oc}$の変動量$V_{\rm oc} (T_1) ~ – ~ V_{\rm oc} (T_0)$はSiの太陽電池の場合おおよそ次式にて計算可能です。

$$ V_{\rm oc} (T_1) ~ – ~ V_{\rm oc} (T_0) \fallingdotseq – ~ 2n (T_1 ~ – ~ T_0) \ \ {\rm mV} \tag{15}$$

またFig.4 (b)より、温度が上昇すると$P_{\rm max}$は低下しています。このとき、最大電力点電圧$V_{\rm mpp}$の変動量は$V_{\rm oc}$の変動量と近い値となるため、温度$T$の増加量に応じて$P_{\rm max}$は減少します。すなわち、$P_{\rm max}$の変動量$P_{\rm max}(T_1) ~ – ~ P_{\rm max} (T_0)$についておおよそ次式が成立します。

$$ P_{\rm max}(T_1) ~ – ~ P_{\rm max} (T_0) \propto – ~ 2n (T_1 ~ – ~ T_0) \tag{16}$$

これらと同様に、温度$T$が低下した際には$V_{\rm oc}$は$T$の変化量に応じて増加し、それに伴って$P_{\rm max}$も増加します。

まとめ

　太陽電池の$I$-$V$特性は日射強度・温度の関数であり、日射強度が変化すると$I$-$V$特性は概形を保ったまま$I$軸方向に平行移動します。一方で、温度変動の影響はマクロには$V$軸方向への平行移動として現れます。
　その結果として、日射強度が増加すると最大電力点電流$I_{\rm mpp}$が大きくなり、最大出力電力$P_{\rm max}$は増大します。一方で、太陽電池モジュールの温度が高くなると最大電力点電圧$V_{\rm mpp}$が低下し、最大出力電力$P_{\rm max}$も低下します。これらの関係をまとめるとTable.1のようになります。

Table.1　日射強度・温度の変化が発電特性に与える影響

$G,T$の変化	短絡電流$I_{\rm sc}$	解放電圧$V_{\rm oc}$	$I$-$V$特性の概形	最大出力電力$P_{\rm max}$
日射強度$G$の上昇	$G$に比例して増加	ほぼ変化なし (僅かに増加)	$I$軸の正方向にシフト	増大
日射強度$G$の低下	$G$に比例して減少	ほぼ変化なし (僅かに減少)	$I$軸の負方向にシフト	減少
温度$T$の上昇	変化なし	減少 (約$-2n ~ {\rm mV/K}$)	$V$軸の負方向にシフト	減少
温度$T$の低下	変化なし	増加 (約$-2n ~ {\rm mV/K}$)	$V$軸の正方向にシフト	増大

　日射強度と最大電力点の関係は非常に良く知られていますが、温度と最大電力点のそれについては日射特性ほど知られておりません。この温度特性に起因する重要な事実として、太陽電池の発電量が最大となる季節が挙げられます。日本の気候において日射条件が最も良くなるのは夏であるため、太陽電池の発電量が最大となる季節は夏であるとのイメージを持たれがちです。しかし、夏は安定した日射強度を得られる一方で著しい温度上により最大電力点電圧$V_{\rm mpp}$が低くなり、結果として取得電力量が低下します。
　そのため、夏よりも気温が低い春のほうが取得電力量が多くなる現象が多々発生します。この様に、太陽電池を利用する際には単に日射条件のみならず、設置場所の気候や環境についても考慮する必要があります。