太陽電池の寄生抵抗がI-V特性に与える影響

太陽電池の等価回路モデルと寄生抵抗
$R_{\rm s}$、$R_{\rm sh}$がI-V特性に与える影響
まとめ
参考文献

太陽電池の等価回路モデルと寄生抵抗

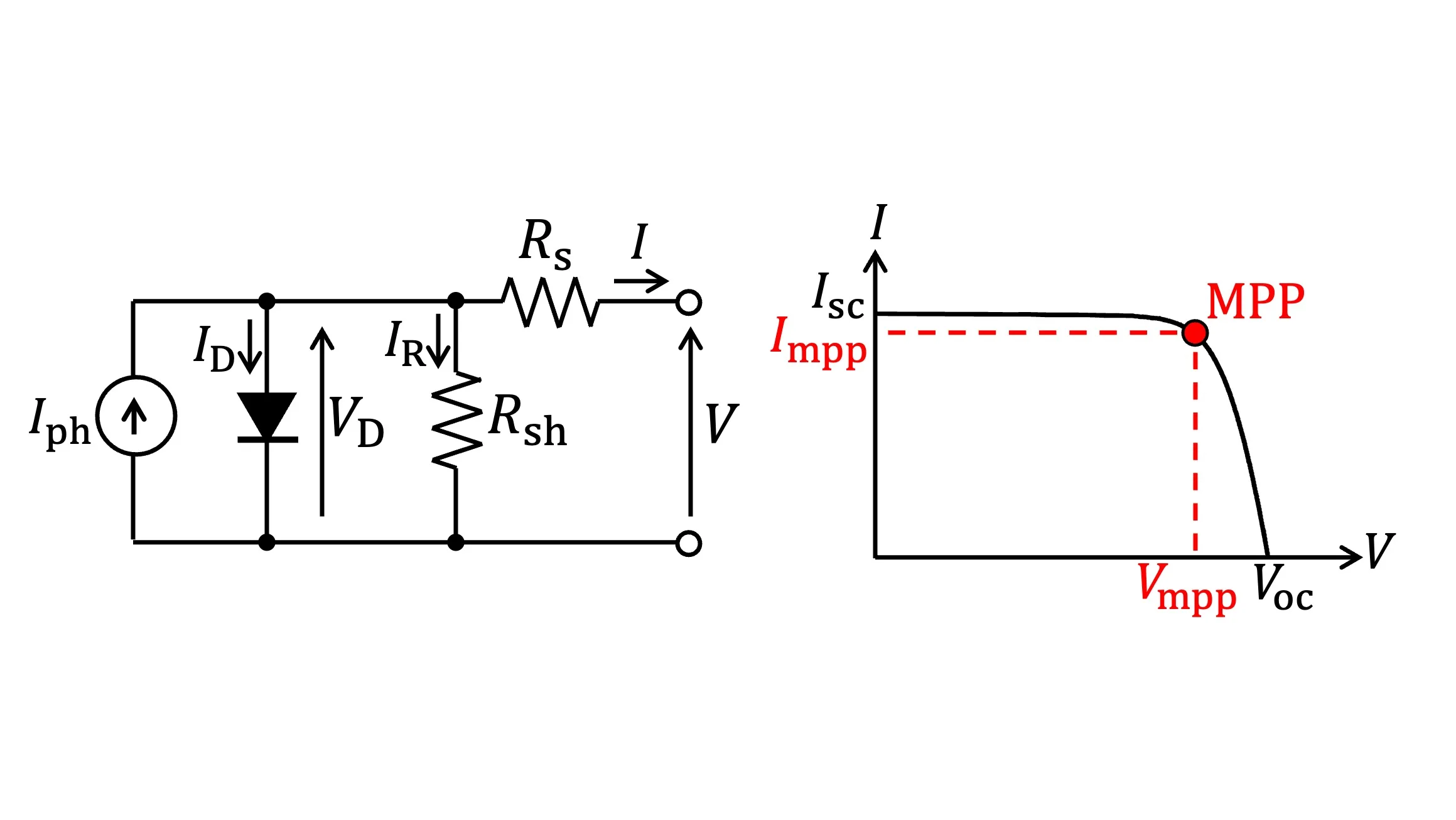
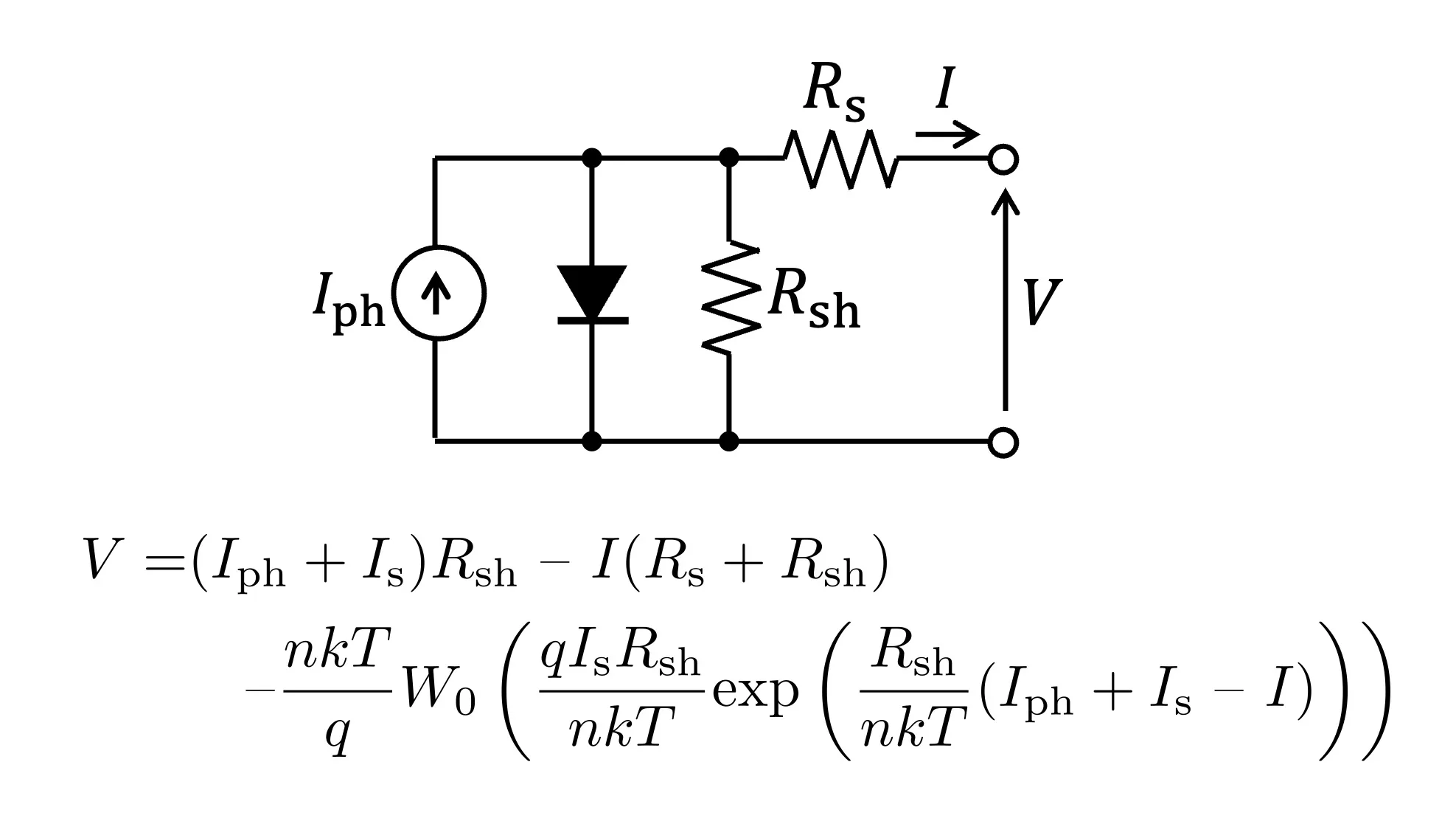
　太陽電池の出力特性はFig.1に示す等価回路としてモデル化されます。Fig.1において$I_{\rm ph}$は光電流、$V_{\rm D}$は内部ダイオードの両端電圧を表します。また、$R_{\rm s}$は直列寄生抵抗(直列等価抵抗)、$R_{\rm sh}$は並列寄生抵抗(並列等価抵抗)です。

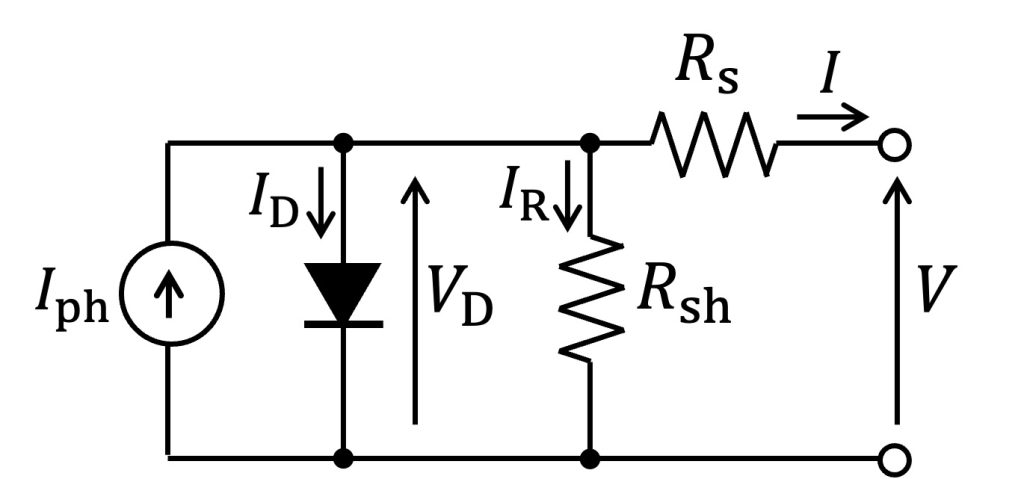
Fig.1 太陽電池の等価回路モデル

Fig.1の回路モデルより、Eq.(1)が立式されます。ここで、$I_{\rm s}$は逆方向飽和電流、$n$はダイオードの理想係数、$k$はボルツマン定数です。

$$ \left \{ \begin{split} I =& I_{\rm ph} ~ – ~ I_{\rm D} ~ – ~ I_{\rm R} \\ =& I_{\rm ph} ~ – ~ I_{\rm s} \left\{ {\rm exp}\left( \frac{qV_{\rm D}}{n kT} \right) -1 \right\} ~ – ~ \frac{V_{\rm D}}{R_{\rm sh}} \\[0.5em] V = & V_{\rm D} ~ – ~ R_{\rm s} I \end{split} \right . \tag{1} $$

出力電圧$V$に関する式を$V_{\rm D}$について解き、出力電流$I$に関する式に代入することで$I$-$V$特性を表すEq.(2)を得ます。

$$ I = I_{\rm ph} ~ – ~ I_{\rm s} \left\{ {\rm exp}\left( \frac{q ( V + R_{\rm s} I ) }{n kT} \right) -1 \right\} ~ – ~ \frac{V + R_{\rm s} I}{R_{\rm sh}} \tag{2} $$

このように、太陽電池の出力特性は5つの等価回路パラメータ$(I_{\rm ph}, I_{\rm s}, n, R_{\rm sh}, R_{\rm s})$により決定されます。本記事では、これらのパラメータの中でも$R_{\rm s}$と$R_{\rm sh}$が$I$-$V$特性に与える影響について取り上げます。

太陽電池の等価回路モデルと$I$-$V$特性の関係に関しては、以下の記事にて詳細に解説を行っているので、併せてご覧下さい。

$R_{\rm s}$、$R_{\rm sh}$がI-V特性に与える影響

　前述のように、太陽電池の$I$-$V$特性は5つの等価回路パラメータ$(I_{\rm ph}, I_{\rm s}, n, R_{\rm sh}, R_{\rm s})$により決定されます。これらのうち、$R_{\rm s}$、$R_{\rm sh}$は$I$-$V$特性上における開放・短絡近傍の傾き($dI/dV$)に影響を与えています。これは太陽電池の$I$-$V$特性に関する非常に重要な性質ですが、あまり認知されていません。本章では、解析的に$dI/dV$を求めることでこれを示します。

まず初めに、$dI/dV$を導出します。Eq.(1)より$I$は$V_{\rm D}$の関数なので、合成関数の微分公式を用いることで$dI/dV$を計算することが可能です[1]。Eq.(1)より$dI/dV$を計算すると、Eq.(3)となります。

$$ \begin{split} \frac{dI}{dV} &= \frac{dV_{\rm D}}{dV} \frac{d I}{dV_{\rm D}} \ &= – \left( 1 + R_{\rm s} \frac{dI}{dV} \right) \left\{ \frac{ q I_{\rm s}}{nkT} {\rm exp}\left( \frac{q V_{\rm D} }{nkT} \right) + \frac{1}{R_{\rm sh} } \right\} \end{split} \tag{3} $$

ここで右辺にも$dI/dV$が現れるので、式を整理して左辺に$dI/dV$をまとめることで次式を得ます。

$$ \frac{dI}{dV} = – \frac{ R_{\rm sh} I_{\rm s} {\rm exp}\left( \frac{q V_{\rm D} }{nkT} \right) + \frac{nkT}{q} }{ R_{\rm s} R_{\rm sh} I_{\rm s} {\rm exp}\left( \frac{q V_{\rm D} }{nkT} \right) + (R_{\rm s} + R_{\rm sh}) \frac{nkT}{q} } \tag{4} $$

このように、$V_{\rm D}$の関数として$dI/dV$が求まります。一方で、$I_{\rm D}$の関数として$dI/dV$を表すこともできます。ショックレーのダイオード方程式より、$I_{\rm D}$と$V_{\rm D}$間の関係は

$$ I_{\rm D} = I_{\rm s} \left\{ {\rm exp}\left( \frac{qV_{\rm D}}{n kT} \right) -1 \right\} \tag{5} $$

にて表されますが、指数関数を左辺に括り出すことでEq.(6)を得ます。

$$ {\rm exp}\left( \frac{qV_{\rm D}}{n kT} \right) = \frac{I_{\rm D} + I_{\rm s} }{ I_{\rm s} } \tag{6} $$

これをEq.(4)に代入することで、$dI/dV$を$I_{\rm D}$の関数として表したEq.(7)が求まります。

$$ \frac{dI}{dV} = – \frac{ R_{\rm sh} \left( I_{\rm D} + I_{\rm s} \right) + \frac{nkT}{q} }{ R_{\rm s} R_{\rm sh} \left( I_{\rm D} + I_{\rm s} \right) + (R_{\rm s} + R_{\rm sh}) \frac{nkT}{q} } \tag{7} $$

・短絡近傍($V\fallingdotseq0$)の傾き

短絡時には出力電圧$V=0$となります。このとき、内部ダイオード電圧は$V_{\rm D} = R_{\rm s} I_{\rm sc}$となりますが、通常$R_{\rm s}$は数Ω以下の値なので内部ダイオードもおおよそ短絡状態となり、$V_{\rm D} \fallingdotseq 0$と近似できます。この条件をEq.(5)に代入することで、短絡近傍の$dI/dV$は次式のように計算されます。

$$ \left. \frac{dI}{dV} \right |_{V=0} \fallingdotseq \left. \frac{dI}{dV} \right |_{V_{\rm D}=0} = – \frac{ R_{\rm sh} I_{\rm s} + \frac{nkT}{q} }{ R_{\rm s} R_{\rm sh} I_{\rm s} + (R_{\rm s} + R_{\rm sh}) \frac{nkT}{q} } \tag{8} $$

$I_{\rm s}$は数百pA~数nAの大きさであるのに対して、熱電圧$nkT/q$は室温300Kにおいて約26mVと$10^{6}$程度もの差があるので、Eq.(8)において分母・分子共に第1項$<$第2項という関係が成立します。また、$R_{\rm s}$は数Ω程度、$R_{\rm sh}$はkΩオーダの大きさなので$R_{\rm s}+R_{\rm sh}\fallingdotseq R_{\rm sh}$です。
従って、短絡状態近傍における$I$-$V$特性のおおよその傾きは次式のように$-1/R_{\rm sh}$で与えられます。

$$ \left. \frac{dI}{dV} \right |_{V=0} \fallingdotseq – \frac{1}{R_{\rm s} + R_{\rm sh}} \fallingdotseq – \frac{1}{R_{\rm sh}} \tag{9} $$

・開放近傍($I\fallingdotseq0$)の傾き

開放時には出力電流$I=0$となります。このとき、等価回路上の内部ダイオードを流れる電流$I_{\rm D}$は次式にて表されます。ここで$V_{\rm oc}$は太陽電池の開放電圧です。

$$ \left. I_{\rm D} \right |_{I=0} = I_{\rm ph} ~ – ~ \frac{ V_{\rm oc} } {R_{\rm sh} } \tag{10} $$

一般に$R_{\rm sh}$はkΩオーダーの値となるので、上式の右辺においては第1項が支配的です。したがって、$I_{\rm D} \fallingdotseq I_{\rm ph}$が成立します。この条件をEq.(7)に代入することで、開放近傍の$dI/dV$は次式のように計算されます。

$$ \left. \frac{dI}{dV} \right |_{I=0} \fallingdotseq \left. \frac{dI}{dV} \right |_{I_{\rm D}=I_{\rm ph}} = – \frac{ R_{\rm sh} \left( I_{\rm ph} + I_{\rm s} \right) + \frac{nkT}{q} }{ R_{\rm s} R_{\rm sh} \left( I_{\rm ph} + I_{\rm s} \right) + (R_{\rm s} + R_{\rm sh}) \frac{nkT}{q} } \tag{11} $$

また、$R_{\rm s}+R_{\rm sh}\fallingdotseq R_{\rm sh}$および$I_{\rm ph} + I_{\rm s}\fallingdotseq I_{\rm ph}$の近似が成り立つので、これらをEq.(11)に適用して整理すると次式となります。

$$ \left. \frac{dI}{dV} \right |_{I=0} \fallingdotseq – \frac{ R{\rm sh} I_{\rm ph} + \frac{nkT}{q} }{ R_{\rm sh} \left( R_{\rm s} I_{\rm ph} + \frac{nkT}{q} \right) } \tag{12} $$

$R_{\rm sh}$は数kΩ、$R_{\rm s}$は数Ω、$I_{\rm ph}$は数A程度の大きさであるのに対して、$nkT/q$は室温300Kにおいて約26mV程度の値です。これにより、Eq.(12)において分母・分子共に第1項$>$第2項という関係が成立します。したがってEq.(12)の分母・分子において第2項が無視できるとすると、開放状態近傍における$I$-$V$特性のおおよその傾きは次式のように$-1/R_{\rm s}$にて与えられます。

$$ \left. \frac{dI}{dV} \right|_{I=0} \fallingdotseq – \frac{1}{R{\rm_s}} \tag{13} $$

注意として、Eq.(12)は第1項と第2項間の大きさがそこまで顕著ではありません。そのため、等価回路パラメータによっては第2項の影響が無視できず、Eq.(13)の近似精度が悪くなる場合があります。

$I$-$V$特性上におけるEq.(9)とEq.(13)の関係を図示するとFig.2のようになります。

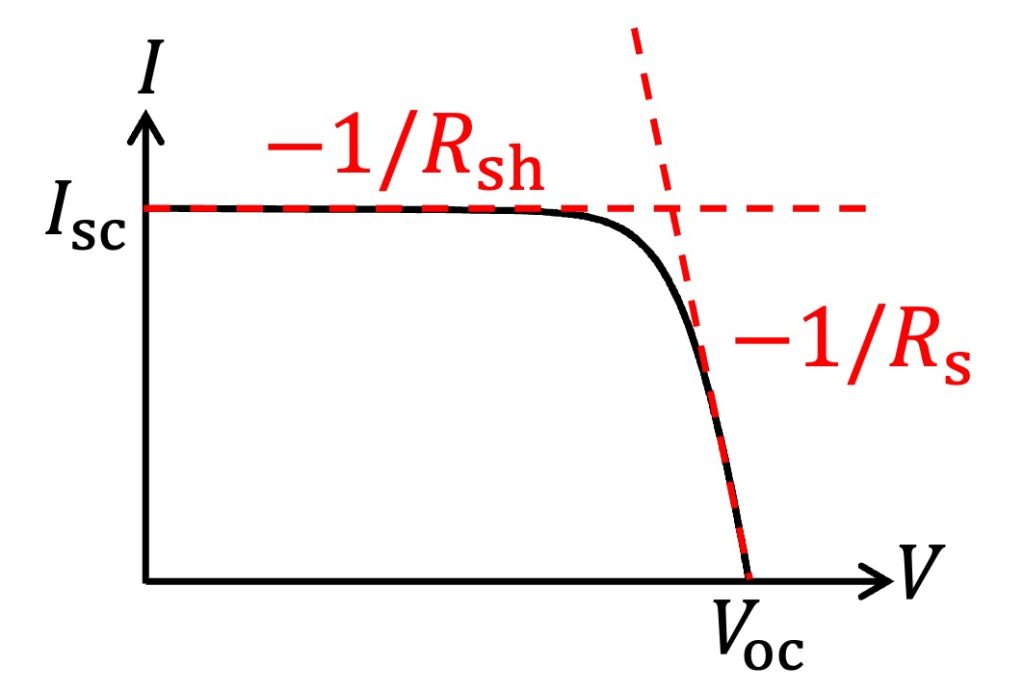
Fig.2 寄生抵抗$R_{\rm sh}$、$R_{\rm s}$が太陽電池のI-V特性に与える影響

まとめ

　本記事では、$R_{\rm s}$、$R_{\rm sh}$により$I$-$V$特性の開放・短絡近傍の傾きが決定されることを説明しました。$I$-$V$特性から等価回路パラメータを同定するためには、等価回路モデルに基づく近似式によりパラメータを計算する、もしくは最小二乗法などを用いてデータ処理を行う必要があります[1]。しかし、本節にて述べた性質を用いる事で$I$-$V$カーブから$R_{\rm s}$、$R_{\rm sh}$のおおよその値を直接読み取ることが可能です。これにより、データシートや実験により計測した$I$-$V$特性などから等価回路パラメータの一部を簡易に読み取ることができます。これは非常に有用かつ特徴的な性質なので、太陽電池を扱う際には覚えておいて損はないでしょう。