太陽電池の等価回路モデルと出力特性
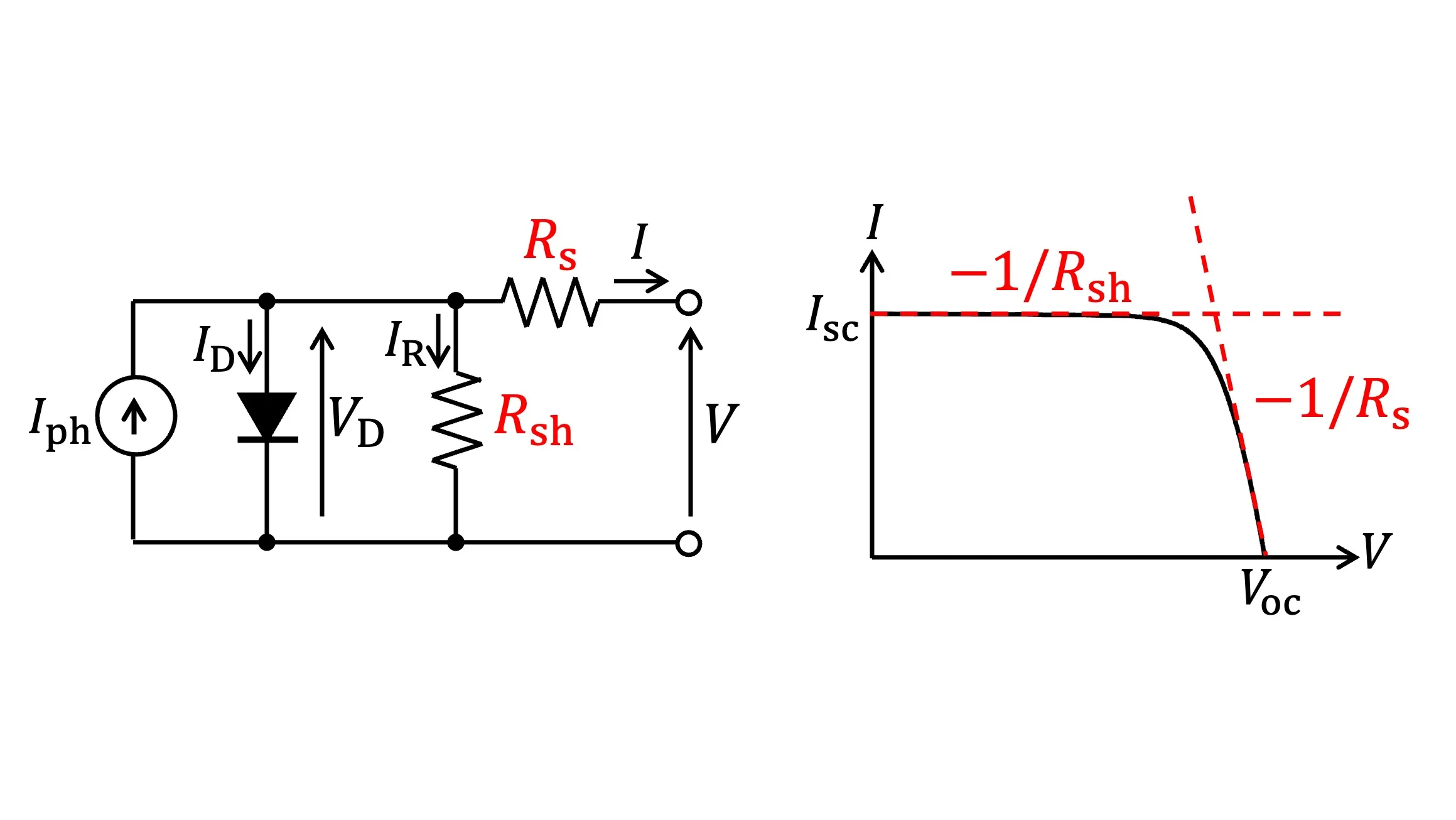
太陽電池はFig.1の等価回路としてモデル化されます[1]。Fig.1において$I_{\rm ph}$は光電流、$V_{\rm D}$は内部ダイオードの両端電圧、$I_{\rm s}$は直列等価抵抗、$I_{\rm sh}$は並列等価抵抗です。
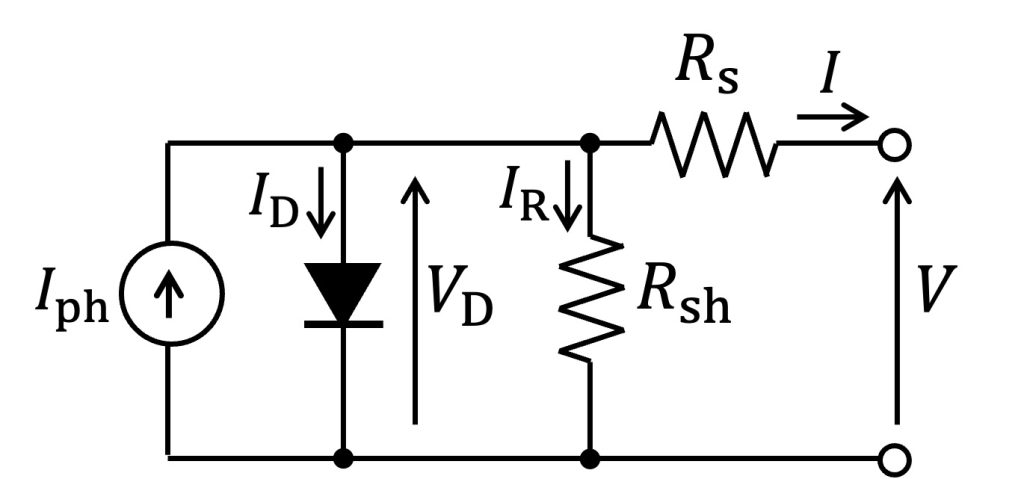
Fig.1 太陽電池の等価回路モデル
Fig.1の回路モデルより、太陽電池の出力特性($I$-$V$特性)はEq.(1)にて表されます。Eq.(1)において、$I_{\rm s}$は逆方向飽和電流、$n$はダイオードの理想係数、$k$はボルツマン定数です。
$$ I = I_{\rm ph} ~ – ~ I_{\rm s} \left\{ {\rm exp}\left( \frac{q ( V + R_{\rm s} I ) }{n kT} \right) -1 \right\} ~ – ~ \frac{V + R_{\rm s} I}{R_{\rm sh}} \tag{1} $$
Fig.1の等価回路モデルについては以下の記事で解説を行っていますので、併せてご参照下さい。
Eq.(1)は太陽電池の$I$-$V$特性を表す数理モデルとしてよく知られていますが、$I$と$V$の関係が陰関数表示となっています。回路モデルという観点ではEq.(1)の表記が本質的ですが、陽関数表示になっている方が便利なケースも存在します。具体的には、数値計算によって$I$-$V$特性をプロットする場合やパラメータの変化が$I$-$V$に及ぼす影響を解析する場合などです。
そこで、本記事ではランベルトのW関数[2]と呼ばれる特殊関数を用いることで、太陽電池の$I$と$V$の関係を陽関数表示にて表現できることを紹介します。また、ランベルトのW関数による陽関数表示を用いることで、開放電圧や短絡電流を解析的に表現できることについて述べます。
ランベルトのW関数
ランベルトのW関数$W(x)$ とは、$y=xe^x$の逆関数であり、次式にて定義される特殊関数です[2][3]。
$$ x = W(x)e^{W(x)} \tag{2} $$
$x$が実数である場合、$W(x)$は2価関数となり、$-e^{-1} \leq x$を定義域とする主枝$W_0(x)$、$-e^{-1} \leq x < 0$を定義域とする分枝$W_{-1}(x)$を持ちます。これは、$-e^{-1} \leq x < 0$においてはとりうる値が2通り($W_0(x)$もしくは$W_{-1}(x)$)存在することを意味します。$x e^x$と主枝$W_0(x)$,分枝$W_{-1}(x)$の関係をFig.2に示します。
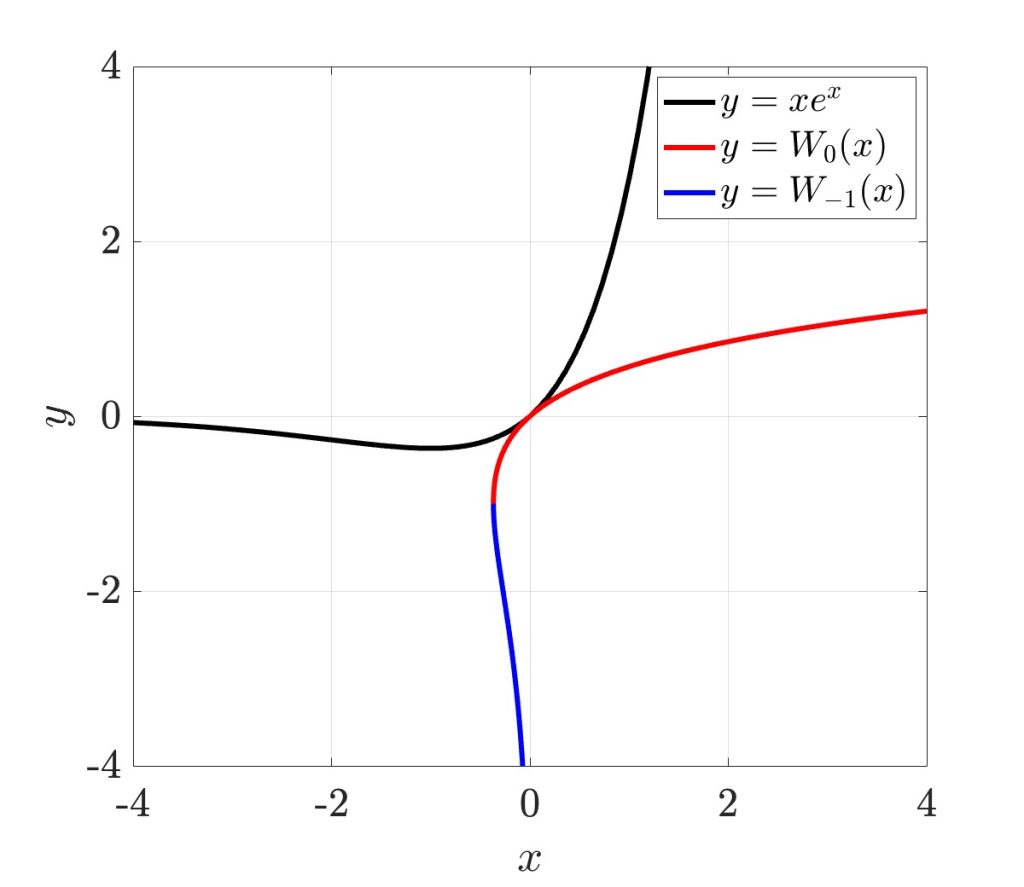
Fig.2 $x e^x$とランベルトのW関数$W(x)$
$W_0(x)$は主枝、$W_{-1}(x)$は分枝を表す
太陽電池の出力特性解析においては$x e^x > 0$となる領域が議論の対象となるため、本記事では主枝$W_0(x)$のみを取り扱います。
なお、ランベルトのW関数は初等関数ではないため、一般には数値的に関数の値を求める必要があります。
しかし、MATLABなどの数値解析ソフトやPythonの数学ライブラリであるSciPyなどにはランベルトのW関数が標準で実装されており、これらを用いることで簡単に計算を行うことができます。Fig.2もMATLABの標準関数を用いて描画しています。
・ランベルトのW関数による超越方程式の求解
ランベルトのW関数を用いる事で、指数関数を含む超越方程式の解を解析的に表現することができます[3]。具体例として、
$$ e^{a x} = b x + c \tag{3} $$
の解$x$はランベルトのW関数$W(x)$を用いて次式のように表現できます。
$$ x = – ~ \frac{c}{b} ~ – \frac{1}{a} W \left( – \frac{a}{b} e^{ – \frac{ac}{b} } \right) \tag{4} $$
このEq.(4)は次章にて$I$-$V$関係の陽関数表示を求める際に使用します。
※Eq.(4)の求め方は記事末尾の付録に記載していますので、興味のある方はご覧ください。
ランベルトのW関数を用いたI-V特性の陽関数表示
ランベルトのW関数を用いて、Eq.(1)を$I$に関する陽関数表示に書き換えます。
Eq.(1)を${\rm exp} \left( q R_{\rm s} I /nkT \right)$について解くことで次式を得ます。
$$ {\rm exp} \left( \frac{q R_{\rm s} I }{nkT} \right) = – \left \{ – \frac{1}{I_{\rm s}} \left( 1 + \frac{R_{\rm s}}{R_{\rm sh}} \right) \right \} {\rm exp} \left( – \frac{q V }{nkT} \right) \left( I – \frac{ I_{\rm ph} + I_{\rm s} + \frac{V}{R_{\rm sh}} }{ 1 + \frac{V}{R_{\rm sh}} } \right) \tag{5} $$
Eq.(5)はEq.(3)の超越方程式と同じ形になっているので、$I$に関する解を求めるとEq.(4)より次式となります[4]。
$$ \begin{split} I = & \frac{ (I_{\rm ph} + I_{\rm s}) R_{\rm sh} ~ – ~ V }{ R_{\rm s} + R_{\rm sh} } \\ & \quad – \frac{nkT}{q R_{\rm s} } W_0 \left( \frac{ q I_{\rm s} R_{\rm s} R_{\rm sh} }{ nkT ( R_{\rm s} + R_{\rm sh} ) } {\rm exp} \left( \frac{ q [ ( I_{\rm ph} + I_{\rm s} ) R_{\rm s} R_{\rm sh} + R_{\rm sh} V ] }{ nkT ( R_{\rm s} + R_{\rm sh} )} \right) \right) \end{split} \tag{6} $$
このように、$I$を$V$の関数として表現することができます[4]。また、逆に$V$を$I$の関数として表すことも可能です。Eq.(1)を${\rm exp}\left( q V / nkT \right)$について解くことで次式を得ます。
$$ {\rm exp}\left( \frac{q V }{nkT} \right) = – \frac{1}{ I_{\rm s} R_{\rm sh} } {\rm exp}\left( \frac{q I R_{\rm s} }{nkT} \right) \left[ V + I ( R_{\rm s} + R_{\rm sh} ) ~ – ~ ( I_{\rm ph} + I_{\rm s} ) R_{\rm sh} \right] \tag{7} $$
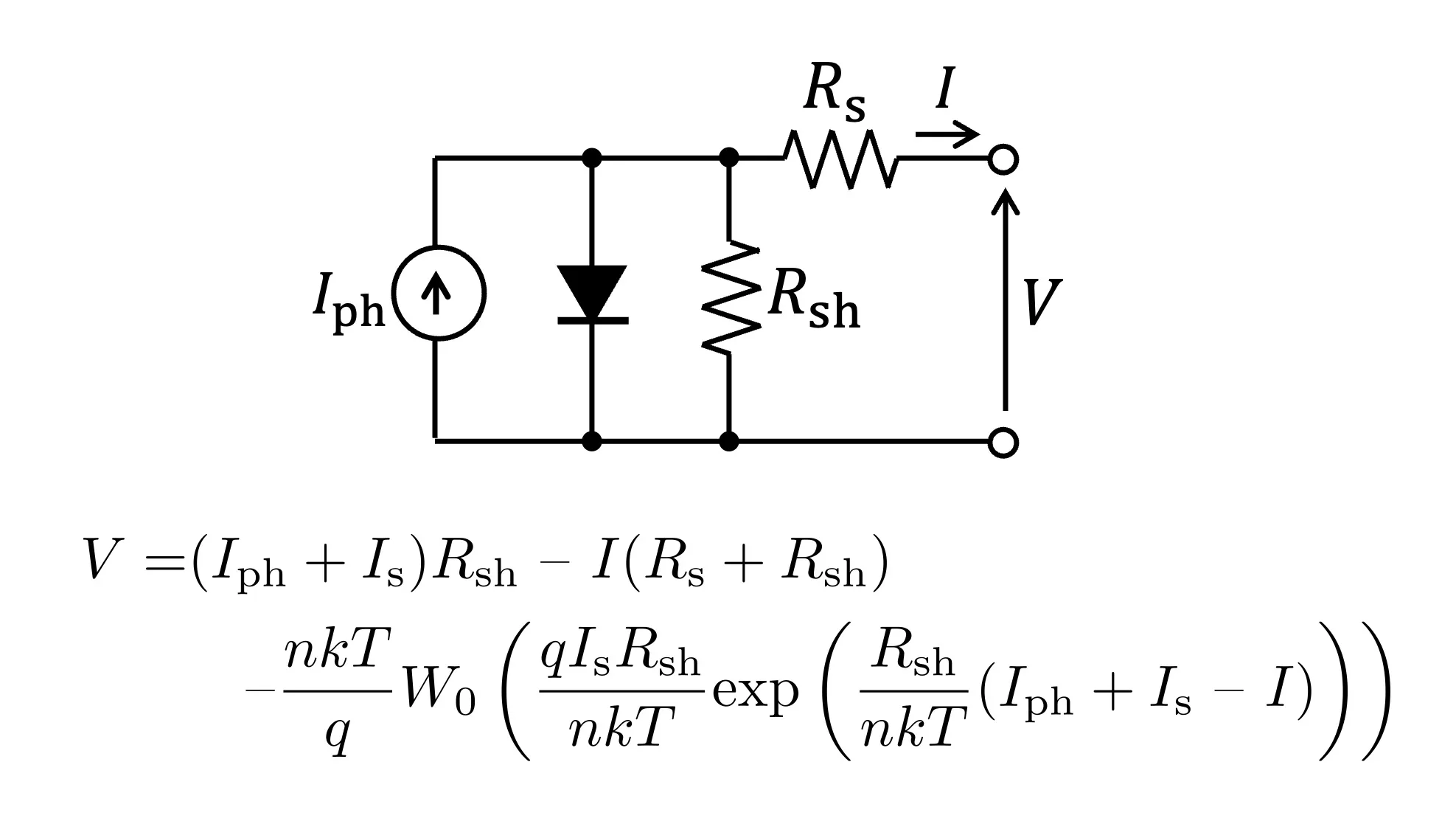
$I$の場合と同様に、Eq.(7)はEq.(3)の超越方程式と同じ形になっているので、$V$に関する解を求めると次式を得ます[4]。
$$ \begin{split} V = & (I_{\rm ph} + I_{\rm s}) R_{\rm sh} ~ – ~ I (R_{\rm s} + R_{\rm sh}) \\ & \quad – \frac{nkT}{q} W_0 \left( \frac{q I_{\rm s} R_{\rm sh}}{nkT} {\rm exp} \left( \frac{R_{\rm sh}}{nkT} (I_{\rm ph} + I_{\rm s} ~ – ~ I ) \right) \right) \end{split} \tag{8} $$
上式のように、$V$を$I$の関数として表現することができます。
ランベルトのW関数による短絡電流と開放電圧の表現
一般に、$R_{\rm sh} \fallingdotseq \infty$、$R_{\rm s} \fallingdotseq 0$などの近似を行わない限りは、Eq.(1)を開放電圧や短絡電流について初等的に解くことはできません。しかし、前章にて述べたようにランベルトのW関数を用いることで、Eq.(1)を$I$もしくは$V$に関する陽関数表示に変形できます。これにより、開放電圧や短絡電流に対して等価回路パラメータがどのように影響するかを明らかにすることができます。
Eq.(6)に短絡状態の条件$V=0$を与えることで、短絡電流$I_{\rm sc}$は次式により表されます。
$$ \begin{split} I_{\rm sc} = \left. I \right|_{V=0} = & \frac{ (I_{\rm ph} + I_{\rm s}) R_{\rm sh} }{ R_{\rm s} + R_{\rm sh} } \\ & \quad – \frac{nkT}{q R_{\rm s} } W_0 \left( \frac{ q I_{\rm s} R_{\rm s} R_{\rm sh} }{ nkT ( R_{\rm s} + R_{\rm sh} ) } {\rm exp} \left( \frac{ q [ ( I_{\rm ph} + I_{\rm s} ) R_{\rm s} R_{\rm sh} ] }{ nkT ( R_{\rm s} + R_{\rm sh} )} \right) \right) \end{split} \tag{9} $$
同様に、Eq.(8)に開放状態の条件$I=0$を与えることで、開放電圧$V_{\rm oc}$は次式により表されます。
$$ V_{\rm oc} = \left. V \right|_{I=0} = (I_{\rm ph} + I_{\rm s}) R_{\rm sh} ~ – ~ \frac{nkT}{q} W_0 \left( \frac{q I_{\rm s} R_{\rm sh}}{nkT} {\rm exp} \left( \frac{R_{\rm sh}}{nkT} (I_{\rm ph} + I_{\rm s} ) \right) \right) \tag{10} $$
このようにランベルトのW関数を導入することで、開放電圧や短絡電流を解析的に表現することができます。これらに限らず、ランベルトのW関数を用いると$I$-$V$特性と等価回路パラメータ間の関係をより詳細に解析することが可能です。
付録:Eq.(4)の求め方
Eq.(2)を適用できる形にEq.(3)の超越方程式を変形します。Eq.(3)の両辺に$-\frac{a}{b}e^{-a \left(x + \frac{c}{b} \right)}$をかけると
$$ – \frac{a}{b} e^{ – \frac{ac}{b} } = -a \left(x + \frac{c}{b} \right) e ^ {-a \left( x + \frac{c}{b} \right)} \tag{11} $$
となり、ここで$~ w = -a \left(x + \frac{c}{b} \right)$とおくことで
$$ – \frac{a}{b} e^{ – \frac{ac}{b} } = w e^ w \tag{12} $$
と変形できます。Eq.(12)にEq.(2)を適用することで、$w$はランベルトのW関数を用いて次のように表すことができます。
$$ w = W \left( – \frac{a}{b} e^{ – \frac{ac}{b} } \right) \tag{13} $$
Eq.(13)の左辺に$~ w = -a \left(x + \frac{c}{b} \right)$を代入し、$x$について解くことで次式を得ます。
$$ x = – ~ \frac{c}{b} ~ – \frac{1}{a} W \left( – \frac{a}{b} e^{ – \frac{ac}{b} } \right) \tag{14} $$
このように、Eq.(3)の解は$W(x)$を用いて解析的に表現できます。
参考文献
[1] 池野孝, 内海淳志, 平地克也, 中川重康, “太陽電池の等価モデルを用いたI-V特性推定型MPPTの提案,” 電気学会論文誌B, vol.138, no.8, pp.514-520, 2018.
[2] R. M. Corless, G. H. Gonnet, D. E. G. Hare, D. J. Jeffrey & D. E. Knuth, “On the LambertW function,” Advances in Computational Mathematics, vol.5, pp.329–359, 1996.
DOI:10.1007/BF02124750
[3] 伊東正人, “物理授業におけるランベルトのW関数の活用法,” 物理教育, vol.67, no.1, pp.22-26, 2019.
DOI:10.20653/pesj.67.1_22
[4] Meetarani Tripathy, Manish Kumar, P. K. Sadhu, “Photovoltaic system using Lambert W function-based technique,” Solar Energy, vol.158, pp.432-437, 2017.
DOI:10.1016/j.solener.2017.10.007


コメント